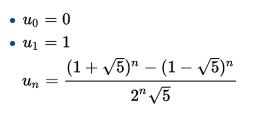Instant catastrophe over all possible directions

The expected number of celestial bodies that will impact this planet in 10 years is the integral of the product of the possible direction along with the probability density function; in essence the sum of the total objects over all possible directions. If the answer is more than one, we will have less chance of survival. We want the probability to be low because we are adding for infinitely possible directions. Then again, catastrophe theory may be fear mongering or a public anxiolytic.

Factor product of two large distinct primes....BY HAND... A challenge!

What is the best way to determine if 91042014201224789 is prime?

Now suppose you are stuck on an island with nothing but a slide rule, any one specific table of your choosing, and an abacus, what is the best way to "by hand" determine if 91042014201224789 is prime?

SPOILER ALERT:
91042014201224789 is a product of two primes, both of which are upwards of 1.6 Million.

If you were stuck on a deserted island with aforementioned tools, how would you best go about factoring 91042014201224789?  The naive, yet easy to implement on a computer/abacus/etc., way is to literally check the remainder when you divide 91042014201224789 by 2, then 3, then 4, then 5, ad infinitum, and see if you can hunt down the smallest factor of 91042014201224789.

As it turns out, if we were to attempt to divide 91042014201224789 by 2, 3, 4, etc., to check for even divisibility (i.e., no remainder), we would have to check every number less than (???).

Or, the TL;DR version: factor 91042014201224789 by hand or prove it is prime.

A number's perspective

A number's perspective, inspired by Edwin A. Abbott's book called Flatland.

You've probably already have heard about binary numbers or hexadecimal numbers. The most common numbers used in this world by humans are base ten, presumably for obvious reasons related to human anatomy.  

Binary numbers are numbers built from powers of two like how base ten (decimal) numbers are built from powers of ten.  They are traditionally written with two symbols such as zero and one.  In base ten, a number represented as 1142 means 2 units, 4 tens, 1 hundred, and one thousand, all added together.  Especially if you've ever dealt with scientific notation, we see that thousands, hundreds, tens, and units (ones) are all powers of ten: a thousand is ten to the third power, a hundred is ten to the second power, ten is ten to the first power, and one is ten to the zero power.

The overall pattern remains the same in other bases.     When you see something like 1011 and if we want to convert binary to base ten, we must first recall two to various powers:

2^0, two to the zero power, is one, 2^1=2, 2^2=4, 2^3=8.

1011 = 1 + 1 x 2^1 + 0 x 2^2 + 1 x 2^3 = 1+2+0+8 = 11 in base ten.

For example, if we were talking about any base z, the meaning is still implied:

(abcd) in base z would be d + c x z^1 + b x z^2 + a x z^3.

What about having other types of numbers as bases?  Some numbers are called rational and others irrational.  The Greeks might have thought a number that repeats a sequence ad infinitum (or, in simpler cases a number whose digits terminate entirely) is more rational than a number whose decimal expansion involves a tail in which no set sequence of digits repeat, i.e., an irrational number.

There are some really famous constants that are irrational: pi, the square root of two, the golden ratio which is somewhat close to the ratio 16:9, and maybe even Euler's constant e.

There is one fact I want to focus on.  If we are not told what the base is, it is pointed to by the representation 10.  This is so because of the expression mentioned earlier.  In the instance of 10, we have 10 = 0 + 1 x z^1 which simplifies to the desired formula for the base z, namely 10 = z which may look nicer if we say z = 10.  In base ten, lo and behold that 10 is the representation, base ten, of ten.  But it is also true in binary.   10 in binary means 0 + 1 x 2^1 which simplifies to 10 = 2 and 2 is the base in binary.

Let's say a few words about base pi.  In accordance with the above paragraph, in base pi, 10 = pi.  In base ten, 3.14 approximates pi but since pi is irrational, in base ten, it's digits will never repeat a set sequence, i.e., it's expansion in base ten is not repeating, in contrast to the rational number 1/3, which involves repeating 3 "forever."

If irrationality means "has no repeating sequence of digits," what about pi's representation in base pi?  In base pi, pi is represented by 10 as we saw earlier.

What's so special about this? Well, 10(base pi) is a terminating representation.  Numbers with terminating representation are called rational.

Pi is irrational in base ten and it is rational in base pi.

So there must be something other that what I've stated that truly characterizes what the difference between a rational and an irrational number is. 

Integer sequences and the OEIS

It is common for integer sequences to appear on intelligence tests. What is the next number? By polynomial interpolation, every finite sequence of integers has many fitting polynomials each of which squirts out a different "next" number. In addition, integer sequences in which at least one number is repeated infinitely often cannot be compressed into a polynomial because nonconstant polynomials aren't wiggly enough to repeat infinitely often. Use of number sequences to provide evidence for intelligence is inherently dubious. Every finite sequence of integers has infinitely many formulas (no one correct/distinguished formula) which fit all the data and most infinite sequences are incompressible (the futility of compressing the incompressible). Finding a formula for the nth term of an integer sequence has become a hobby of mine. Here is one example of the types of ideas that pop up: the Fibonacci sequence. What is the one billionth number? The follow your nose method would be to calculate the sum of the previous two terms approximately one billion times. Another method involves the golden ratio and eliminates the need to compute about a billion intermediate calculations. Setting parameters phi to be the golden ratio and psi we shall set to the negative reciprocal of phi, we know the following:

At first this formula for the Fibonacci sequence may look unduly complex for something as easy as adding the two previous numbers. However, this formula is perfect for the question, "what is the next number." There is one step to calculating the billionth term of Fibonacci: substitute one billion for n in the above equation. It almost feels like magic when all the square roots vanish leaving an integer. Though it is easier to just add two previous numbers, without a formula like the above one would have to calculate all terms of the sequence to answer the question "what is the billionth number".

My take on dimensions, numbers, and general relativity

Sounds like basically the four dimensions used in GR are all mathematically pretty much the same on a fundamental level. It's not like the fourth dimension of the model space in GR (which is R^4) acts much different from the first three. The metric that gives distance between two points in space-time, however, does do something different for the fourth dimension than it does for the first three. The square of distance infinitesimal element ds^2 is, by the transfer principle of logic, in addition to Pythagoras' theorem, is not merely

dx^2 + dy^2 + dz^2 + dt^2

I think that it's dx^2 + dy^2 + dz^2 - k * dt^2

for some value of k (I have no idea what k means physically). However, it didn't have to be the fourth one we write with a -k in front; it could have been the first one or the third one. What's necessary is that exactly three of the dimensions have positive metric but exactly one of the four must be multiplied by some negative number.

I don't think that GR is able to answer the question why 3 must have positive sign and 1 must have negative sign.

So, in that small technical sense of how points' distances between each other, the time dimension is only distinguishable as something who contributes negatively to distance squared. And if you remember your complex analysis, supposing there is more timelike distance than spacelike distance between two points, that means the distance itself will be a non-real, complex number.

The distance for two points only differing in the first three coordinates is never non-real. If the two points are the same point in 3-space, but if they aren't the same then they differ in the time-coordinate; in that case, the distance between them is imaginary. This tells us that the concept of measure/distance is dependent upon a sense in which space and time do not work the same exact way, the way, say, dimension 2 and dimension 1 work.

But let me say a word on that foul word, imaginary. Imaginary numbers get a bad rap. First of all, imaginary is a word describing contrast with what are known as real numbers. The real numbers are visualized and thought of as a line, well, points on a line. ALL imaginary numbers are are the numbers that are visualized and thought of as points in a PLANE.

Once you define how to add, subtract, divide, and multiply two complex numbers (i.e., basically imaginary numbers), the plane becomes a field just like the real numbers are. The complex numbers just have one more dimension than the real numbers; then not surprisingly, the complex numbers are specified by two coordinates.

I think complex numbers get a bad rap because of their unfortunate appellation. We owe the quirky, psychological descriptors labels for types of numbers to the Greeks. These numbers have colorful descriptions like irrational, transcendental, real, imaginary, negative, etc, etc.. The way the story was told to me it seems the Greeks basically couldn't fathom irrational numbers as ever possibly "actually" existing. The first way to need irrational numbers is when trying to deduce width and length from area. If a square can have 4 units of area and a 3-square can have 9 units of area, then why can't there be a square having 5 units of area? This needs the square root of 5 to be invoked.

At any rate, the complex numbers are essentially not a whole lot different from irrational numbers in a sense. Note that these numbers can solve the area problem when the area is negative the same way irrational numbers can solve the area problem when the area is not a perfect square number.

Oh yeah, perfect, that is another heavily-human word.

My music projects

The disagreement with Max Tegmark

Max Tegmark is my favorite living scientist.  I think that's a sign that you are a scientist or a musician or artist or poet: when you have a favorite one of that discipline.

(Not only if you get published, sell a record, or discover something new.)

He and I are at odds in one critical intersection of musings.  He thinks reality must be "computable" and that only Godelian-complete "space" is allowed to be part of reality.  He said straight up: Brian but formal languages are not mathematical objects.

Technically he said that Formal Systems aren't mathematical objects. That must be why he has it circumscribed by a red annulus.

Two things. Mathematical democracy and simpler theory compared to one in which only parallels which exist who meet certain strict criteria.

Formal systems, special cases of formal language, have the same ontological primacy as sets, strings, Neptune, and the HyperWebster which may be the context of any TOE. That means the hyperwebster is self similar and recursive (fractal).

The theory of formal languages indicates that formal language theory provides a type of model for classical set theory (i.e., ZF set theory).  Thus sets are contingent upon them (and vice versa) for their existence.

So if Tegmark believes in a level 4 universe where mathematical structures are parallels equipped by the rules of the structure (in essence), that mathematical existence equals physical existence, then there are more general structures than the ones in set theory which represent parallels larger than he considers to exist.

Yet parallel UNIVERSES should be as all-inclusive as possible, and that's not to mention mathematical democracy, that all structures exist.  Show the rules of formal languages to most mathematicians and I bet they would say it's no more or less a structure than groups... And if that caliber of peoples and organizations thinks formal systems (such as investigated by well known logician Raymond Smullyan) are mathematical objects.

For what it's worth, I think formal languages (hence, formal systems; the basis for his map of structure) are mathematical objects.  This is not to mention that this way it obeys Occam's razor: the two theories have intersecting conclusions (reality is a mathematical structure), but mine doesn't arbitrarily discriminate as to whether they are "computable" which is rather anthrocentric.

So we have that (1) Formal languages are mathematical objects and (2) formal languages are more general than "computable structures."  Computable structures would be a type of parallel but not a parallel universe. Give it a fancy name like quasi-parallel universe or quasi-parallel.  Since formal languages encompass computable structures, they are more towards the Universe.