It is common for integer sequences to appear on intelligence tests. What is the next number? By polynomial interpolation, every finite sequence of integers has many fitting polynomials each of which squirts out a different "next" number. In addition, integer sequences in which at least one number is repeated infinitely often cannot be compressed into a polynomial because nonconstant polynomials aren't wiggly enough to repeat infinitely often.
Use of number sequences to provide evidence for intelligence is inherently dubious. Every finite sequence of integers has infinitely many formulas (no one correct/distinguished formula) which fit all the data and most infinite sequences are incompressible (the futility of compressing the incompressible).
Finding a formula for the nth term of an integer sequence has become a hobby of mine. Here is one example of the types of ideas that pop up: the Fibonacci sequence. What is the one billionth number? The follow your nose method would be to calculate the sum of the previous two terms approximately one billion times. Another method involves the golden ratio and eliminates the need to compute about a billion intermediate calculations. Setting parameters phi to be the golden ratio and psi we shall set to the negative reciprocal of phi, we know the following:
At first this formula for the Fibonacci sequence may look unduly complex for something as easy as adding the two previous numbers. However, this formula is perfect for the question, "what is the next number." There is one step to calculating the billionth term of Fibonacci: substitute one billion for n in the above equation. It almost feels like magic when all the square roots vanish leaving an integer. Though it is easier to just add two previous numbers, without a formula like the above one would have to calculate all terms of the sequence to answer the question "what is the billionth number".
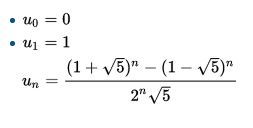
No comments:
Post a Comment